Bring maths and English to life with DoodleLearning
The award-winning educational apps for EYFS, KS1 & KS2
Bring maths and English to life with DoodleLearning
The award-winning educational apps for EYFS, KS1 & KS2

Bring maths and English to life with DoodleLearning
✔ Trusted by 10,000+ teachers
✔ Loved by 1,000,000+ children
✔ Proven to boost confidence and ability


Discover DoodleLearning
Meet Doodle, the suite of programmes revolutionising the way children learn!
Covering the core areas of maths and English, our four apps create every child a personalised learning experience tailored to their needs, helping to boost their confidence and ability.
DoodleMaths
Filled with 40,000+ interactive exercises, DoodleMaths explores numerical reasoning and problem solving, giving children core skills they can use in the classroom and beyond!Find out more
DoodleTables
Going beyond instant recall, DoodleTables helps children to understand the relationships between numbers, enabling them to truly master their times tables.
Find out more
DoodleEnglish
Covering spelling, punctuation, grammar and comprehension, DoodleEnglish builds key literacy skills and explores language in real-life contexts, bringing the curriculum to life.Find out more
DoodleSpell
DoodleSpell helps children to understand the meaning behind words and how to use them in sentences, improving their vocabulary and taking them beyond ‘look, cover, write, check’.Find out more
What makes Doodle special
What makes Doodle special

Filled with thousands of interactive exercises, games and rewards, Doodle transforms learning into a rewarding activity that children always look forward to
Using real classroom experience, every question and explanation has been carefully crafted by our team to suit all types of learner, ensuring that Doodle is accessible to all
Doodle guides children through all core content at a pace that’s right for them, supporting what they’re learning in school and ensuring continual progression
By setting work at just the right level, Doodle lets all children work without supervision, helping to boost their confidence and resilience
Doodle automatically marks each child’s work and displays their results in an online hub, providing in-depth insights and making it easy to celebrate their hard work
Designed to be used for just a few minutes a day, Doodle can be used offline on all devices, making it ideal for busy schedules!

*Based on answering 18 questions a day. Data from baseline assessment results of 60,282 children between Feb 2021-Feb 2022.


Using Doodle for 10 minutes a day is proven to double a child's rate of progression
*Based on answering 18 questions a day. Data from baseline assessment results of 60,282 children between Feb 2021-Feb 2022.
Using Doodle for 10 minutes a day is proven to double a child's rate of progression
*Based on answering 18 questions a day. Data from baseline assessment results of 60,282 children between Feb 2021-Feb 2022.

Learning with Doodle
Learning with Doodle

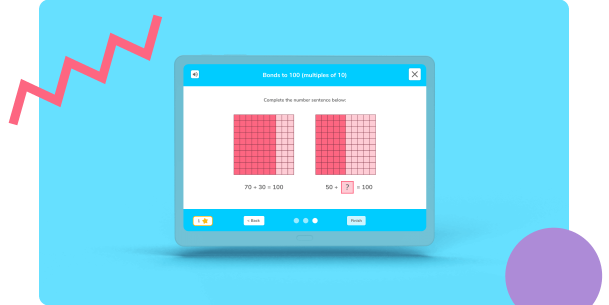
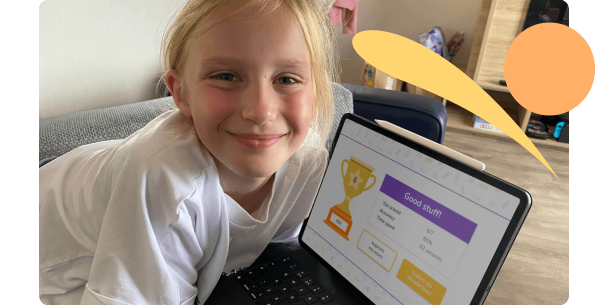


Engaging questions
Interactive explanations
A reward system like no other
Fun features
Holiday Challenges
From measuring angles with a protractor to tracing letters, all of Doodle’s exercises are fully-interactive, ensuring that learning is always fresh and engaging.
Children learn best by doing; that’s why Doodle’s questions are accompanied by short hands-on summaries rather than lengthy descriptions
By rewarding effort over ability, Doodle encourages even the least confident and disengaged learners to keep up their hard work
With in-app badges, educational games and virtual rewards to enjoy, Doodle encourages daily practice and boosts each child’s confidence a little every day
Learners can earn real life rewards by taking part in Challenges, seasonal events designed to keep children motivated and prevent learning loss
Our mission

Made by education specialists
We’re passionate about creating immersive, affordable learning experiences that can be enjoyed by all. Our apps are specifically designed to break down any anxieties around maths and English, helping every child to feel totally brilliant!
Always on hand
Our Customer Support Team are always on hand to help with any questions that you may have. Schools can also receive the support of a dedicated support advisor to provide training, advice and ongoing support.


Making a difference
From fundraising for local charities to providing Doodle to those in disadvantaged areas, we’re passionate about supporting our local and global community to make education accessible to all.
Our mission

Made by education specialists
We’re passionate about creating immersive, affordable learning experiences that can be enjoyed by all. Our apps are specifically designed to break down any anxieties around maths and English, helping every child to feel totally brilliant!
Always on hand
Our Customer Support Team are always on hand to help with any questions you may have. Schools can also receive the support of a dedicated advisor to provide training, advice and ongoing support.


Making a difference
From fundraising for local charities to providing Doodle to those in disadvantaged areas, we’re passionate about supporting our local and global community to make education accessible to all.
Our mission

Made by education specialists
We’re passionate about creating immersive, affordable learning experiences that can be enjoyed by all. Our apps are specifically designed to break down any anxieties around maths and English, helping every child to feel totally brilliant!

Always on hand
Our Customer Support Team are always on hand to help with any questions you may have. Schools can also receive the support of a dedicated advisor to provide training, advice and ongoing support.

Making a difference
From fundraising for local charities to providing Doodle to those in disadvantaged areas, we’re passionate about supporting our local and global community to make education accessible to all.












